计算机科学入门 ​

今天，我们来看一位对计算机理论贡献巨大的人，计算机科学之父—— 阿兰·图灵 。

阿兰·马蒂森·图灵 于 1921 年出生在伦敦，从小就表现出惊人数学和科学能力，他对计算机科学的建树始于 1935 年，当时他是剑桥国王学院的硕士生，他开始解决德国数学家 大卫·希尔伯特 提出的问题，叫 Entscheidungsproblem （德语），即 可判定性问题 。

是否存在一种算法，输入正式逻辑语句，输出准确的 是 或 否 答案？也就是告诉它问题，它告诉你答案。

如果这样的算法存在，可以回答比如 是否有一个数大于所有数？ 。

图灵机 ​

美国数学家 阿隆佐·丘奇 于 1935年 首先提出解决方法，他开发了一个叫 Lambda 演算 的数学表达系统，证明了这样的算法 * 不存在* ，虽然 Lambda 演算能表示任何计算，但它使用的数学技巧 难以理解和使用 。

同时在大西洋另一边，阿兰·图灵 想出了自己的办法来解决 可判定性问题 ，提出了一种假想的计算机，现在叫 图灵机 。

图灵机提供了简单又强大的数学计算模型，虽然用的数学不一样，但图灵机的计算能力和 Lambda 演算一样，同时因为图灵机更简单，所以在新兴的计算机领域更受欢迎。

图灵机是一台 假想 计算设备，因此我们不需要去深究如何实现，因为它只是一个思想，实际不存在这样的机器。

他有 无限长 的纸带，可以储存符号。

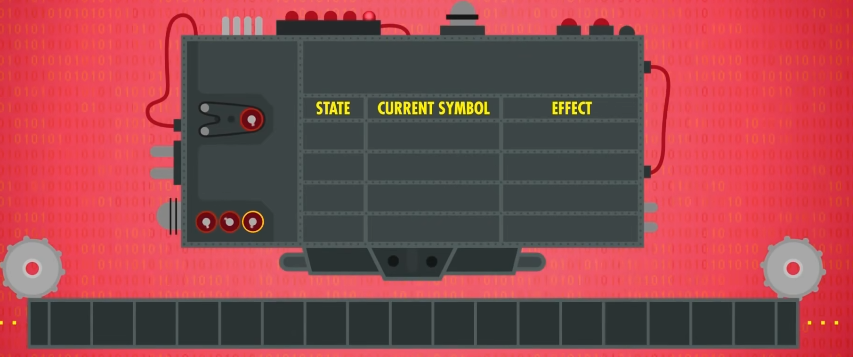
还有一个读写头，可以 读取 和 写入 纸带上的符号。

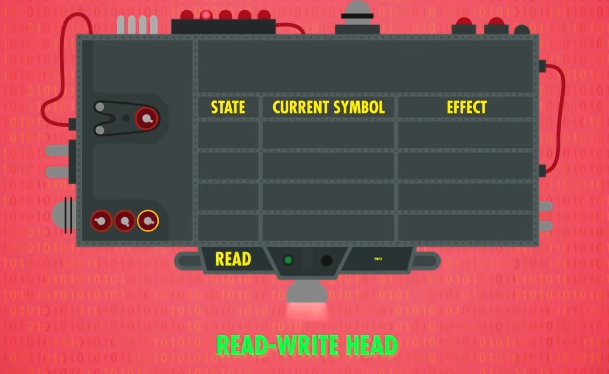
还有一个状态变量，保存当前的状态。

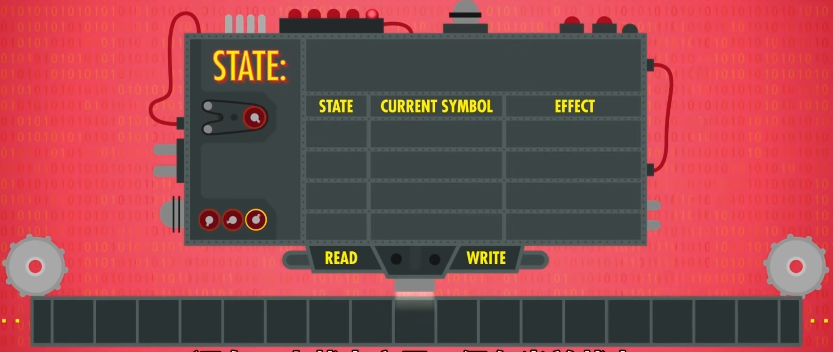
还有一个规则，根据 当前状态+读写头读取的符号 ，决定机器做什么。可能是在纸带写入一个符号，或改变状态，或把读写头移动一格。

现在我们让图灵机读一个以零结尾的字符串，并计算 1 的出现次数 是不是偶数。

如果是, 在纸带上写一个 1 ，如果不是，在纸带上写一个 0 。

比如 1 1 1 1 0 中有 4 个 1 ，因此是偶数，在纸带上写 1 ； 1 1 1 1 1 0 中有 5 个 1 ，因此是奇数，这时在纸带上写 0 。

让我们来看看用图灵机怎么实现。

首先，我们需要确定规则，这个很像逻辑门的 真值表 ，我们需要列出所有情况，并指定在这些情况下图灵机应该怎么做。

• 当前状态分为 奇数 和 偶数 ，这代表着目前出现的 1 的个数是奇数还是偶数。
• 读写头读取的符号分为 1 和 0 ，如果读到 1 则需要改变当前状态，因为奇数和偶数是 交替 出现的，并将读写头右移，读取下一个字符；读到 0 则停止，并写下答案。

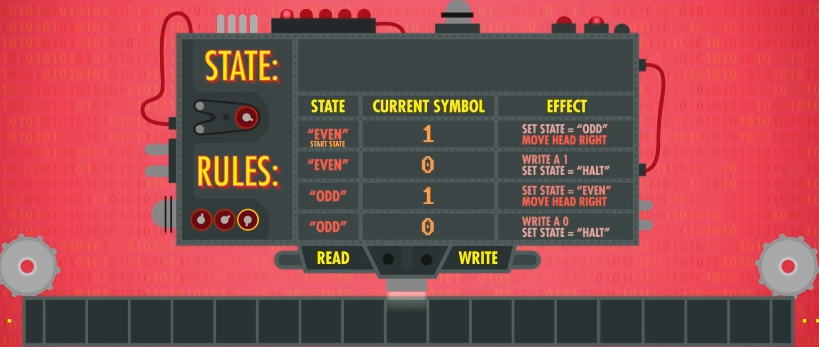
让我们来试一下，在纸带上写下一个字符串，并将当前状态设为 偶数 （虽然 0 非奇非偶，但是 1 是奇数，每一次读取都会改变状态，因此需要让它符合）。

第一个读到的字符是 1 ，因此切换状态为奇数，并移动到下一格。

第二个读到的字符是 1 ，因此切换状态为偶数，并移动到下一格。

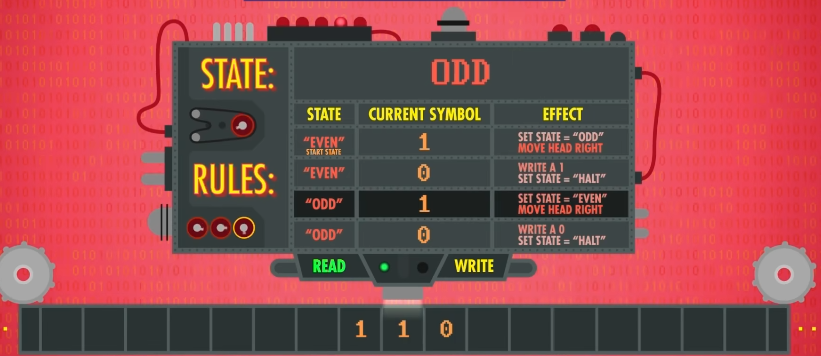
第三个读到的字符是 0 ，因此不再移动，当前状态为偶数，因此写下 1 。

图灵证明了这个简单假想机器，如果有足够时间和内存，可以执行任何计算，它是一台 通用 计算机。

所以图灵机是很强大的计算模型，事实上，就可计算和不可计算而言，没有计算机比图灵机更强大，和图灵机一样强大的，叫 图灵完备 。每个现代计算系统都是 图灵完备 的。

停机问题 ​

为了回答可判定性问题，他把图灵机用于一个有趣计算问题：停机问题 。

简单说就是，给定图灵机描述和输入纸带，是否有算法可以确定，机器会永远算下去还是到某一点会停机？

比如，刚才我们的 判断字符串中出现的 1 的次数是奇数还是偶数 ，当我们输入 110 的时候最后是停机的；如果我们让它判断 圆周率有没有尽头 那估计是永远不会停机的。

有没有办法在不执行的情况，弄清会不会停机？

一些程序可能要运行好几年，所以在运行前知道会不会出结果很有用。

图灵通过一个巧妙逻辑 矛盾 证明了停机问题是无法解决的，

想象有一个假想图灵机，输入：问题的描述 + 纸带的数据，输出 Yes 代表会 停机 ，输出 No 代表 不会 。

给这台机器一个有趣的名字叫 H，来自 "停机"（halt） 的第一个字母。

如果有个程序， H 无法判断是否会 "停机" ，意味着 "停机问题" 无法解决。

为了找到这样的程序，图灵用 H 设计了另一个图灵机，如果 H 说 会停机 ，那么新机器会永远运行；如果 H 说 不会停机 ，那么让新机器输出 No，然后 "停机" 。

这实质上是一台和 H 输出相反的机器：如果程序不停机，就停机；如果程序停机，就永远运行下去。

现在我们将这个机器看作一个 整体 。

接下来我们将它运行的 结果 重新放入。

它的结果当然只有两种答案：停机 和 不停机 。

如果是 停机 ，那么 H 结果是 YES ，第二个机器会永远运行，整体 不停机 。

如果是 不停机 ，那么 H 结果是 NO ，第二个机器会停机，整体 停机 。

这个结果是自相矛盾的，这是一个 悖论 ，所以 H 无法判断是否会 "停机" ，意味着 "停机问题" 不能用图灵机解决。

无论有多少时间或内存，有些问题是计算机无法解决的。——丘奇-图灵论题

破解英格玛机 ​

从1936年到1938年在丘奇指导下，他在普林斯顿拿到博士学位，毕业后回到剑桥。

1939年后不久，英国卷入第二次世界大战，图灵的才能很快被投入战争。

事实上，在战争开始前一年，他已经在英国政府的密码破译学校兼职，那是位于 "布莱切利园" 的一个密码破译组织。

他的工作内容之一是破解德国的通信加密，特别是 英格玛机 加密的信息。

简单说，英格玛机会加密明文，如果输入字母 H-E-L-L-O ，机器输出 X-W-D-B-J ，这个过程叫 加密 。

文字不是随便打乱的，加密由 "英格玛机" 顶部的齿轮组合决定，每个齿轮有26个可能位置。

机器前面还有插板，可以将两个字母互换，总共有上十亿种可能，根本没法手工尝试所有组合。

如果你有"英格玛机"，并且知道正确的齿轮和插头设置，输入X-W-D-B-J ，机器会输出 hello 。

幸运的是，英格玛机和操作员不是完美的，一个大缺陷是：字母加密后绝不会是自己 。H 加密后绝对不是 H 。

图灵接着之前波兰破译专家的成果继续工作，设计了一个机电计算机，叫 Bombe 。

利用了这个缺陷，它对加密消息尝试多种组合，如果发现字母解密后和原先一样，我们知道英格玛机决不会这么做，这个组合会被跳过，接着试另一个组合。

Bombe 大幅减少了搜索量，让破译人员把精力花在更有可能的组合，比如在解码文本中找 常见的德语单词 。

德国人时不时会怀疑有人在破解，然后升级英格玛机，比如加一个齿轮，创造更多可能组合，他们甚至还做了全新的加密机。

整个战争期间，图灵和同事在布莱切利园努力破解加密，解密得到的德国情报，为盟军赢得了很多优势，有些史学家认为他们把战争减短了好几年。

战后 ​

战后，图灵回到学术界为许多早期计算机工作做出贡献，比如 曼彻斯特 1 号 ，一个早期有影响力的存储程序计算机（在内存里储存程序的计算机）。

但他最有名的战后贡献是 人工智能（Artificial Intelligence） ，这个领域很新，直到1956年才有名字。

图灵测试 ​

1950 年，图灵设想了未来的计算机：拥有和人类一样的智力，或至少难以区分。

图灵提出如果计算机能欺骗人类相信它是人类，才算是智能，这成了智能测试的基础，如今叫 图灵测试 。

想像你在和两个人沟通不用嘴或面对面，而是来回发消息，可以问任何问题，然后会收到回答，但其中一个是计算机，如果你分不出哪个是人类，哪个是计算机，那么计算机就 通过 了图灵测试。

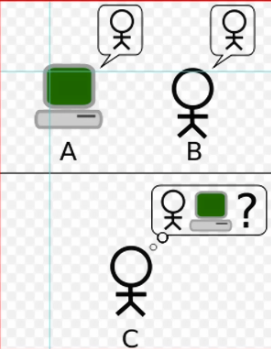
这个测试的现代版叫 "公开全自动图灵测试，用于区分计算机和人类"（a completely automated public turing test to tell computers and humans apart） ，简称 验证码（Captcha），防止机器人发垃圾信息等。

落幕 ​

图灵那个时代，同性恋是违法的，英国和大部分国家都是。

1952 年调查他家的入室盗窃案时，向当局暴露了他的性取向，被起诉 "行为严重不检点"。

图灵被定罪，有2个选择：1. 入狱 2. 接受激素来压制性欲。

他选了后者，部分原因是为了继续学术工作。

但药物改变了他的情绪和性格，图灵于 1954 年服用含氰化物的苹果自尽，年仅 41 岁。

图灵奖 ​

图灵奖（Turing Award），全称A.M.图灵奖（ACM A.M Turing Award），是由美国计算机协会（ACM）于1966年设立的计算机奖项，名称取自艾伦·麦席森·图灵（Alan M. Turing），旨在奖励对计算机事业作出重要贡献的个人 。图灵奖对获奖条件要求极高，评奖程序极严，一般每年仅授予一名计算机科学家。图灵奖是计算机领域的国际最高奖项，被誉为 计算机界的诺贝尔奖 。