计算机科学入门
算法(Algorithm)是指解题方案的准确而完整的描述,即使结果一致,有些算法会更好,一般来说,所需步骤越少越好,不过有时我们也会关心其他因素,比如占多少内存。
算法 一词来自波斯博识者 阿尔·花拉子密 ,1000 多年前的代数之父之一。

算法入门
先来看一个问题:从 1 加到 N 。
首先最简单的办法当然是每一次用 循环 ,这样做速度是最慢的。
第二种办法我们可以在开始建一张 表 ,每一次循环都将 结果 放入表内,这样不会影响多少速度,但之后我想取 小于 N 的答案时非常快。比如:第一次要求加到 100 ,但是循环 结束 后表内已经有 100 个数据,第二次我需要加到 88 ,我可以 直接 从表内取出数据而不需要再次循环,当然了,我需要加到 200 的话也不再需要从 1 开始重新加。这是一种 用空间换时间 的方法。
还有更快的方法吗?
当然有,我们可以直接使用高中学过的 等差数列 公式。
这样无论 N 是多少,只需要 一次运算 就可以得出结果。
这就是算法的好处。
算法的特征
- 有穷性(Finiteness):算法的有穷性是指算法必须能在执行 有限个 步骤之后终止。
- 确切性(Definiteness):算法的每一步骤必须有 确切 的定义。
- 输入项(Input):一个算法有 0 个或多个输入,以刻画运算对象的初始情况。
- 输出项(Output):一个算法有一个或多个输出,以反映对输入数据加工后的结果。
- 可行性(Effectiveness):算法中执行的任何计算步骤都是可以被分解为基本的可执行的操作步骤,即每个计算步骤都可以在 **有限时间 ** 内完成。
排序算法
记载最多的算法之一是 排序 ,比如给名字、数字排序,计算机科学家花了数十年发明各种排序算法。
TIP
排序算法将在专门的算法模块中详细阐述。
冒泡排序
这是最简单的排序算法之一,也是大多数人入门算法学习的 第一个 算法。
它也是一种 稳定 排序算法。其实现原理是重复扫描待排序序列,并比较每一对相邻的元素,当该对元素顺序不正确时进行交换。一直重复这个过程,直到没有任何两个相邻元素可以交换,就表明完成了排序。
一般情况下,称某个排序算法稳定,指的是当待排序序列中有相同的元素时,它们的相对位置在排序前后不会发生改变。
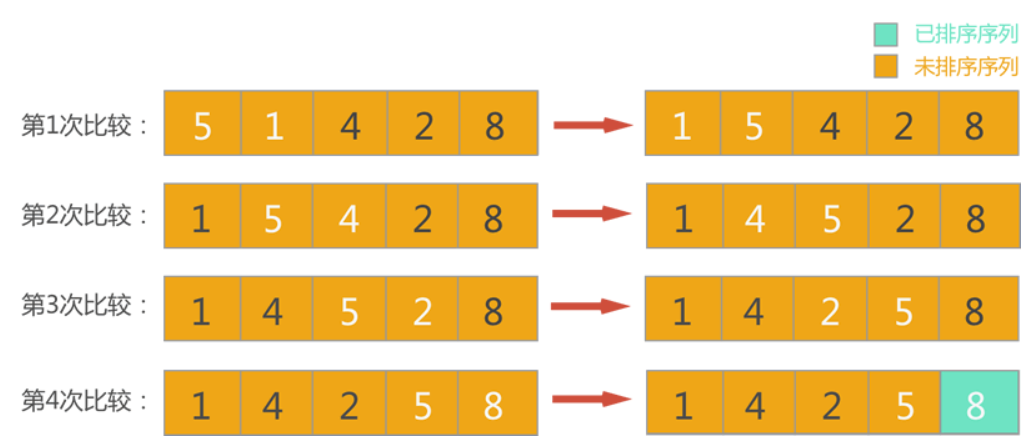
从图中可以看到,经过 两两比较 ,从待排序序列中找出了 最大数 8,并将其放到了待排序序列的尾部,并入已排序序列中。
冒泡排序的特点就是:每一次排序将 待排序列 中最大的数上浮至第一位。
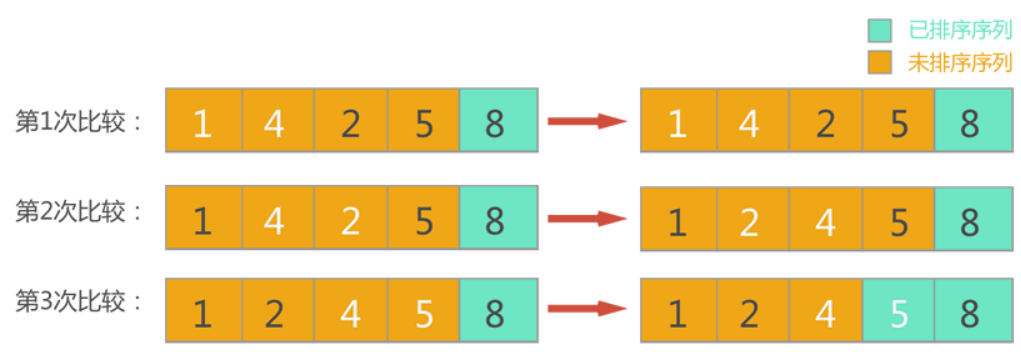
第二次循环找出了 待排序列 中的最大数,也就是整体序列中第二大的数 5 。

以此类推,到只剩最后一个元素的时候,也就不再需要比较了,因为它就是最小的数字。
时间复杂度
算法的时间复杂度是指算法所需要的 计算工作量 ,当然了这个工作量是指在 最坏的情况下 ,有时候待排序列还没有开始排序就已经是有序的了,这样算出的工作量没有意义。
刚才所说的冒泡排序中,我们排了 5 个数字,最坏的情况是每一次循环都是第一位数字上浮到最后,这时操作次数是 4 + 3 + 2 + 1 。
如果是 10 个数字的话就是 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 。
不难发现这是一个 等差数列 ,因此使用求和公式。
可以得出冒泡排序在输入量为 n 时,所需的操作数量为:
只保留最高次项并去掉系数,因为在数据量足够大的时候,最高次项对整体的影响是最大的。
并将结果用 O() 包裹,因此冒泡排序的时间复杂度为:
这也被称为 大 O 表示法 。
算法的时间复杂度不是 精确 的时间,而是一个大体 趋势 。
常见复杂度有常数时间O(1),对数时间O(logn),线性时间O(n),线性对数时间O(nlogn),二次时间O(n^2)等。
空间复杂度
空间复杂度是对一个算法在运行过程中占用内存空间大小的量度,可以对程序运行中需要多少内存有个预先估计,依然使用大 O 来表示。
TIP
空间复杂度的计算会用到具体代码,因此将在专门的算法板块进行阐述。