计算机科学入门
数据存在内存里的格式就是 数据结构 ,我们希望数据是结构化的,方便读取。
TIP
这一章只是简略了解数据结构,详细阐述请见专门的数据结构模块。
数组
数组(Array)也叫列表(list)或向量(Vector),不同的编程语言有不同的叫法。
数组的值一个个 连续 存在内存里,就像这样。
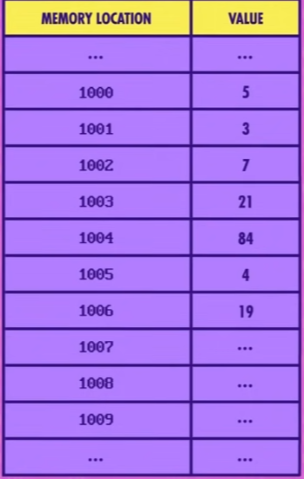
为了拿出数组中某个值,我们要指定一个下标(index),大多数编程语言里,数组下标都从 0 开始,用方括号 [ ] 代表访问数组。
在上图中,如果这个数组叫 j ,想要取出数组的第一个元素 5 ,只需要用 j[0] ,就可以了。
如果想相加数组 j 的第一个和第三个元素,并把结果存在变量 a ,可以这样写:
a = j[0] + j[2]a = j[0] + j[2]记住,数组的下标是从 0 开始的!很容易混淆 "数组中第 5 个数" 和 "数组下标为 5 的数",它们不是一回事。
字符串
数组根据里面储存数据的类型不同可以分为整型数组(int)、浮点数数组(float)、字符数组(char)等。
而其中字符数组比较特殊。
我们都知道使用 ASCII 码 可以表示 26 个英文字母,但是一个单词由好多字母组成,这时候我们需要将字符拼在一起,也就是将一个个字符 放入字符数组 中。
在用字符数组表示字符串时,计算机需要知道在哪停下,因此需要一个标志,在大多数编程语言中为 \0 。
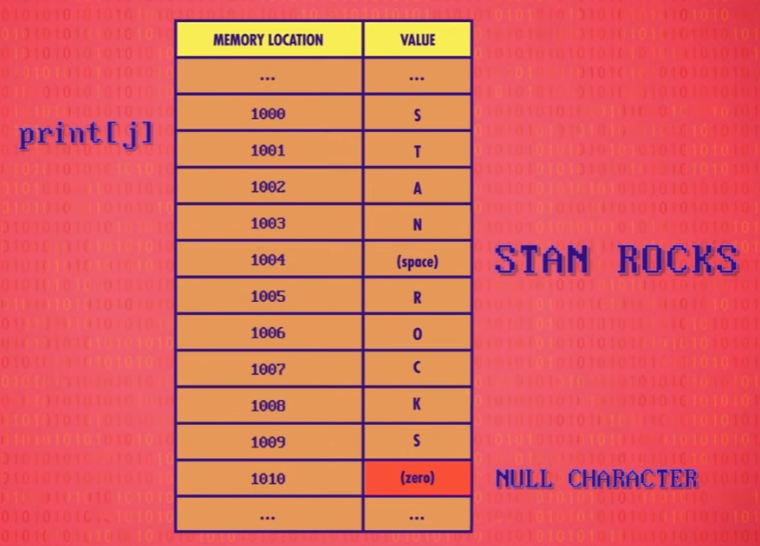
使用字符数组表示字符串的时候非常麻烦,而且计算机经常处理字符串,所以有很多函数专门处理字符串,在大多数编程语言中,String 也是基本数据类型之一,其底层正是字符数组。
TIP
在 C 语言中没有 String 类型,因此在 C 语言中想要使用字符串需要自己实现。
二维数组
我们可以用数组做一维列表,但有时想操作 二维数据 ,比如电子表格,或屏幕上的像素,那么需要 矩阵(Matrix)。
可以将一维数组看成数轴,只需要一个数字就可以表示。

而二维数组就是坐标系了,需要两个数字表示,需要给出 x 和 y 才能找到那个点,在二维数组中需要两个中括号。
二维数组在内存中是这样的。
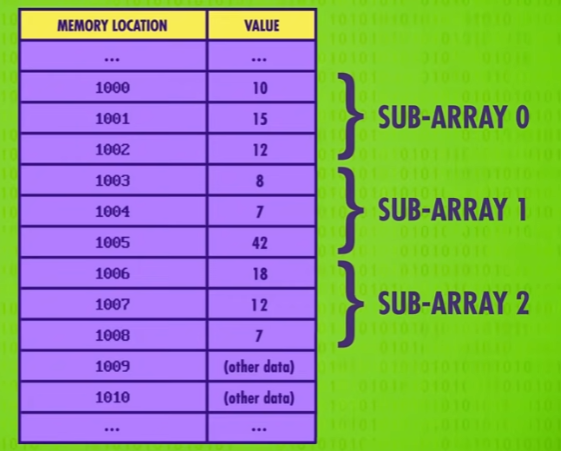
假如这个数组叫做 j ,我们在第一个中括号 [ ] 中输入要访问的 SUB-ARRAY ,在第二个中括号 [ ] 中输入 SUB-ARRAY 中的几号元素。
比如 j[0][1] 表示 SUB-ARRAY 0 中的第二个元素,在上图中是 15 。
TIP
二维数组的两个下标同样从 0 开始。
更高维的数组
一维数组可以看成是数轴,二维数组可以看成是坐标轴,以此类推,三维数组可以看成是 空间坐标系 。
同理,需要有三个值 x 、 y 、z 在可以在空间坐标系中找到那个点,在三位数组中也需要 三个中括号 ,比如 j[1][0][2] 。
以此类推,还可以有四维数组、五维数组、六维数组等等,只要你需要的话。
可惜的是,超过三维数组后无法再使用 具象 的描述,四维数组只存在于抽象中(因为我们的世界属于三维)。
结构体
目前我们只存过单个数字/字符,存进数组或矩阵,但有时, 把几个有关系的变量存在一起, 会很有用,多个变量打包在一起叫 结构体 (Struct)。
我们可以将不同数据类型的数据放在一起,比如银行账户名是你的名字,是 字符串 (String),余额是 浮点数 (float),我们可以将这些数据放在一起。

当然了,结构体也可以作为 数组 。

存结构体的数组,和其它数组一样,创建时就有 固定大小 ,不能动态增加大小,还有,数组在内存中按 顺序存储 ,在中间插入一个值很困难。
链表
节点
我们来看一个结构体,叫 节点(node),它存一个变量一个指针(pointer)"指针" 是一种特殊变量,指向一个内存地址,因此得名。

循环链表
我们可以将节点连在一起,做成一个 链表 ,在这里,每一个节点的指针指向下一个节点的地址。
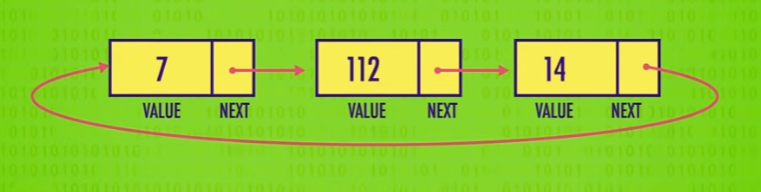
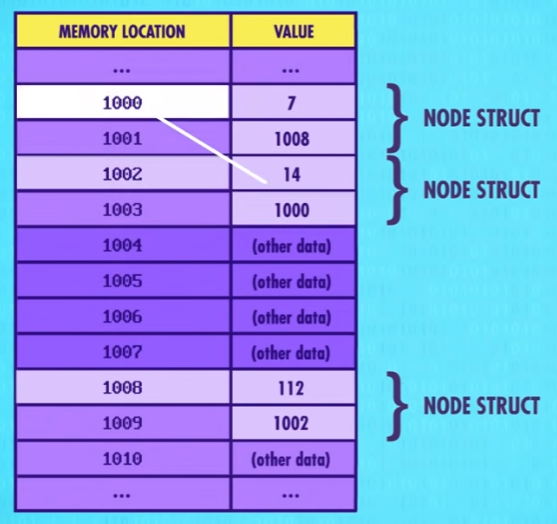
它在内存中是这样的,链表不同于数组,它在内存中的地址不一定是连续的。
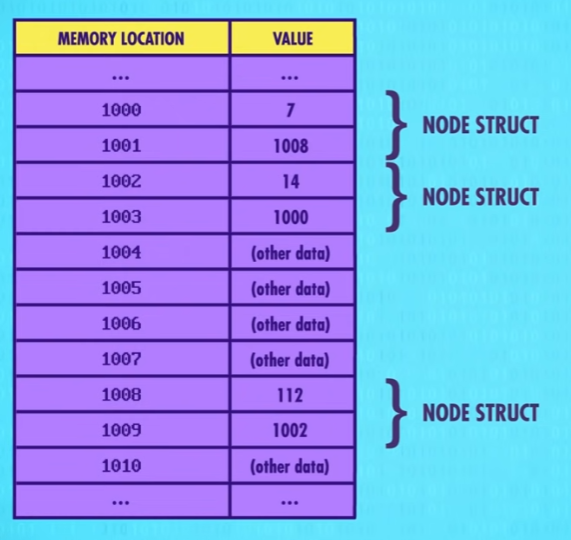
在每一个节点中,不仅有数据,还有下一个节点的地址。
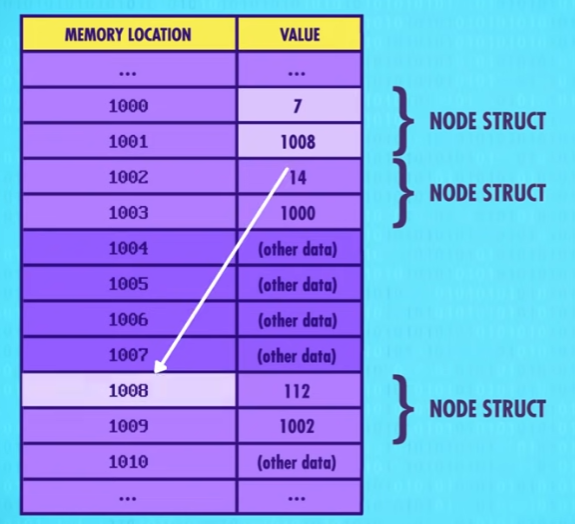
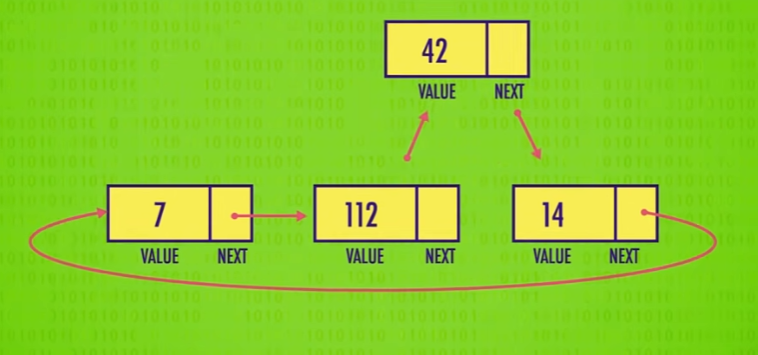
在这个链表中,最后一个节点中指针指向的又是第一个节点,因此所有节点连起来是一个 循环 ,又叫 循环链表 (circular)。
链表尽头
但链表也可以是非循环的,最后一个节点的指针为 null 就可以表示链表尽头。
链表的好处
链表想要加入或删除数据非常简单,因为每个节点在内存中不一定是连续的,因此我们不需要管它在哪。
比如新增数据,我们只需要将上一个节点的指针指向新插入的数据,将新插入数据的指针指向原来链表的下一个地址就可以了。
队列
队列是一种特殊的结构,它可以用链表来实现,它的特点是 先进先出 (First-In First-Out),简称 FIFO 。
在队列里的数据就像是过隧道的车,先进隧道的车会先从隧道里出来(速度相同的时候)。

数据进入队列叫做 入队 (enqueue),数据从队列中出去叫做 出队 (dequeue)。
TIP
队列将在专门的数据结构模块详细阐述。
栈
栈是一种特殊的结构,它可以用链表来实现,它的特点是 先进后出 (Last-In First-Out),简称 LIFO 。
在栈中的数据就像是在羽毛球桶里的羽毛球,第一个扔进去的球在最下面,当我们拿球的时候,第一个拿到的球是最后一个投进去的。

数据进入栈叫做 入栈 (push),数据从栈中出去叫做 出栈(pop)。
TIP
栈将在专门的数据结构模块详细阐述。
树
将节点像这样连接的数据结构叫做 树 ,其中最上面的节点叫做 根节点 (root)。
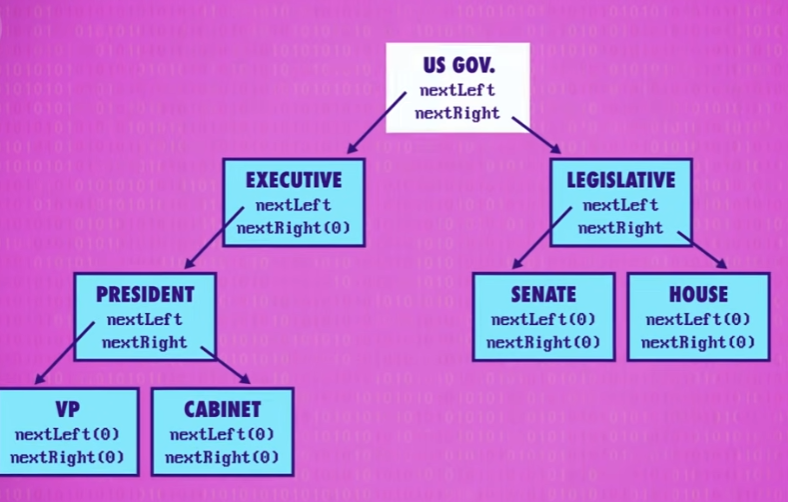
在它之下的这些节点叫做 子节点 (children)。
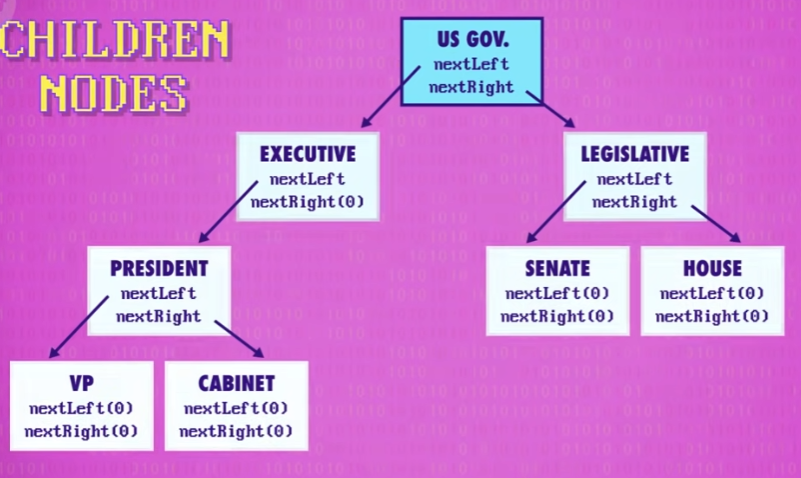
任何子节点的直属上层节点,叫 父节点(parent node),比如 SENATE 和 HOUSE 的父节点是 LEGISLATIVE 。
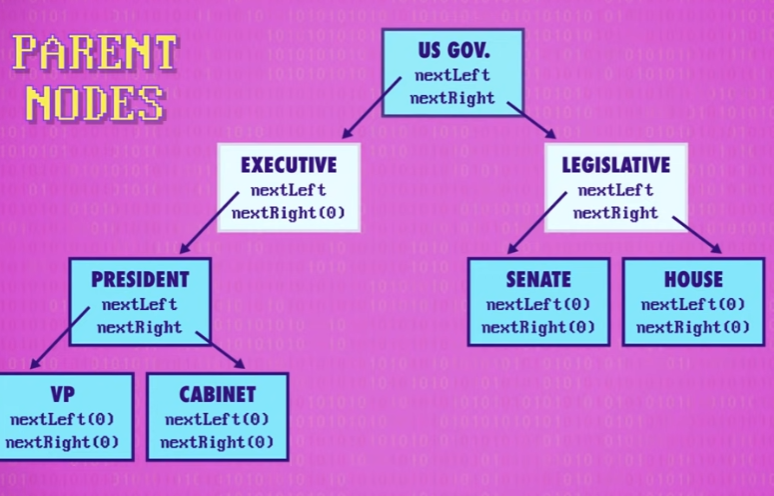
没有任何 子节点 的节点叫做 叶节点 (Leaf Nodes)。
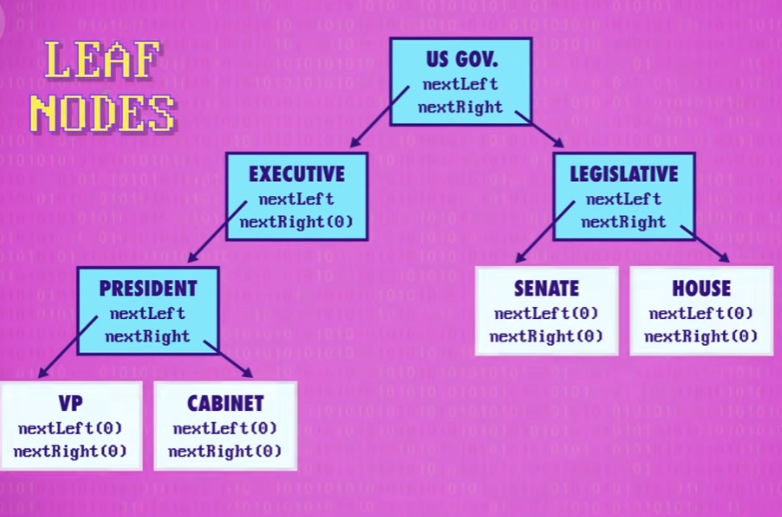
结点的度:一个结点含有子树的个数称为该结点的度。
树的度:一棵树中,所有结点度的最大值称为树的度。
树的深度:一棵树中节点的最大深度就是树的深度,也称为 高度 。
非终端节点或分支节点:度不为0的节点。
兄弟节点:具有相同父节点的节点互称为兄弟节点。
节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推。
堂兄弟节点:双亲在同一层的节点互为堂兄弟。
子孙:以某节点为根的子树中任一节点都称为该节点的子孙。
森林:由m棵互不相交的树的集合称为森林。
像这样拥有最多 2 个子节点的树叫做 二叉树 ,当然也有四叉树、五叉树等等。
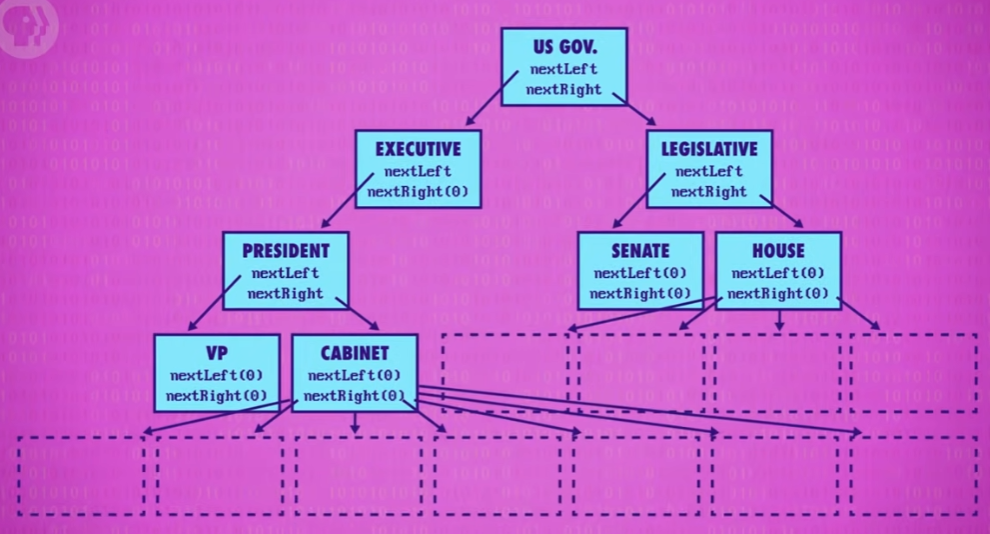
TIP
树的子树是不相交的,除了根节点外,每个节点有且仅有一个父节点。
图
树的子树一旦相交,则叫做 图 (graph )。
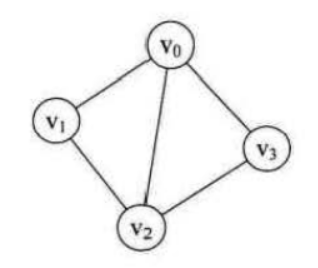
TIP
树和图将在专门的数据结构模块中详细阐述。