计算机科学入门 ​

在过去我们聊了很多计算机安全话题，但事实是，世上不存在 100% 安全的系统，总会有 漏洞 存在，而且安全专家知道这一点，所以系统架构师会部署 多层防御 ，用多层不同的安全机制来阻碍攻击者。

有点像城堡的设计一样，首先要避开弓箭手，穿过护城河，翻过城墙，避开热油，打败守卫，才能达到王座。

不过我们这里要说的是，计算机安全中最常见的防御形式， 密码学 （Cryptography）。

cryptography 一词，来自 crypto 和 graphy ，大致翻译成 秘密写作 ，为了加密信息，要用 加密算法 (Cipher)把 明文 转为 密文 ，除非你知道如何解密，不然密文看起来只是一堆乱码。

把明文转成密文叫 加密 (encryption)，把密文恢复回明文叫 解密 (decryption)。

替换加密 ​

凯撒加密 ​

加密算法早在计算机出现前就有了， 朱利叶斯·凯撒 用如今我们叫 凯撒加密 （Caesar cipher）的方法来加密私人信件，他会把信件中的字母向前移动 三个 位置，所以 A 会变成 D ， brutus 变成 euxwxv 。

为了解密，接收者要知道，用了 什么算法 和 要偏移的字母位数 ，有一大类算法叫 替换加密 （substitution ciphers），凯撒密码是其中一种。

算法把每个字母替换成其他字母，但有个巨大的缺点是， 字母的出现频率是一样的 。

举个例子，E 在英语中是最常见的字母，如果把 E 加密成 X ，那么密文中 X 的出现频率会很高，熟练的密码破译师可以从 **统计数据 ** 中发现规律，进而破译密码。

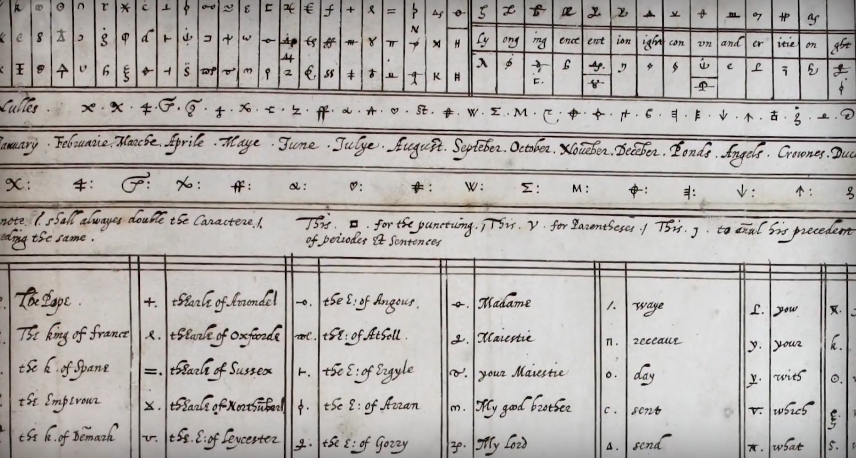
1587 年，正因为一个 替换加密 的密文被破译，导致杀伊丽莎白女王的阴谋暴露，使得玛丽女王被处决。

移位加密 ​

另一类加密算法叫 移位加密 （permutation ciphers），我们来看一个简单例子叫 列移位加密 （columnar transposition cipher）。

我们把明文填入网格，网格大小我们这里选择 5x5 。

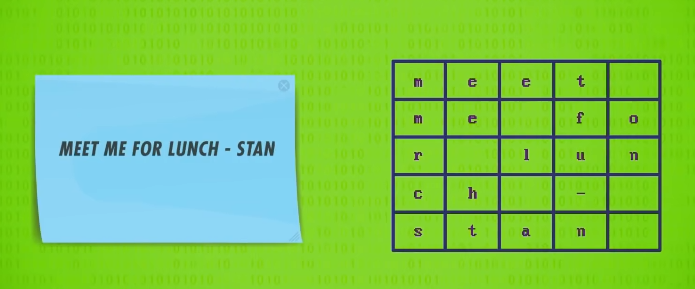
为了加密信息，我们 换个顺序 来读。比如从左边开始，从下往上，一次一列。

加密后字母的排列不同了，解密的关键是，知道读取方向和网格大小是 5x5 ，就像之前，如果接收者知道密文和加密方法，才能解密得到原始消息。

英格玛机 ​

到了 1900 年代，人们用密码学做了加密机器，其中最有名的是德国的 英格玛 （Enigma），纳粹在战时用英格玛加密通讯信息。

正如之前说过，Enigma 是一台像打字机的机器，有键盘和灯板，两者都有完整的字母表，而且它有一系列 转子 (rotros)，是加密的关键。

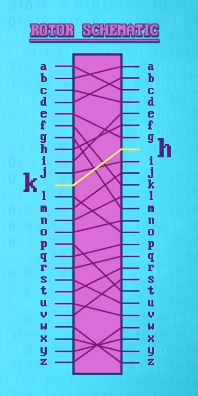
首先，我们只看一个转子，它一面有 26 个接触点，代表 26 个字母，然后线会连到另一面， 替换 字母。

如果输入 H ， K 会从另一边出来。

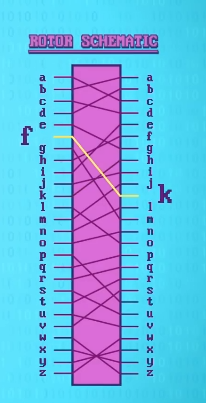
如果输入 K ， F 会从另一边出来，以此类推。

这个字母替换过程你应该听起来很熟悉：它是 替换加密 ！

但 英格玛 (Enigma)更复杂一些，因为它有 3 个或更多转子， 一个转子的输出作为下一个转子的输入 。

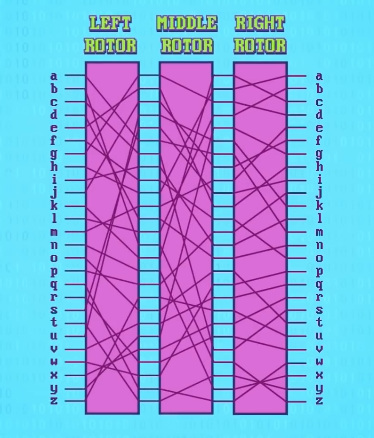
转子还有 26 个起始位置，还可以按 不同顺序 放入转子，提供更多字母替换映射。

转子之后是一个叫 反射器 （reflector）的特殊电路，它每个引脚会连到另一个引脚，并把信号 发回 给转子。

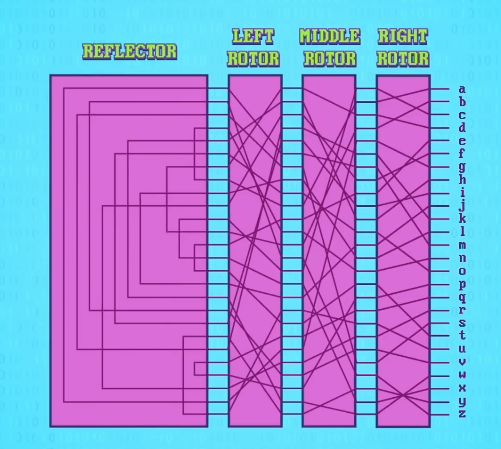
最后，机器前方有一个 插板 （plugboard） 。

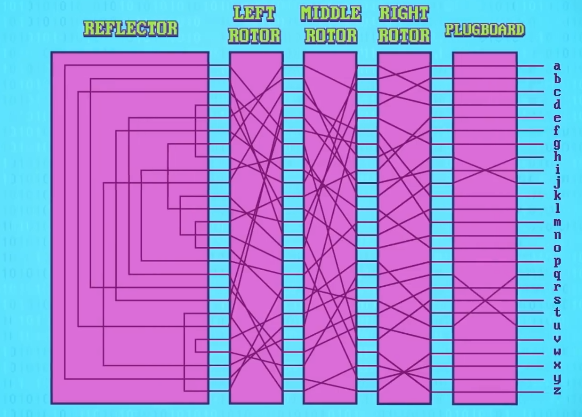
可以把输入键盘的字母预先进行 替换 ，又加了一层复杂度。

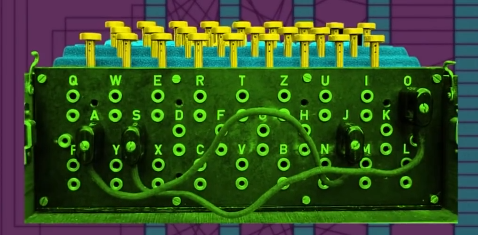
让我们用这里的简化版电路，加密一些字母，如果我们按下 H 键，电流会先通过插板，然后通过转子，到达反射器，然后回来转子，回来插板，并照亮键盘灯板的字母 L ， H 就加密成了 L 。

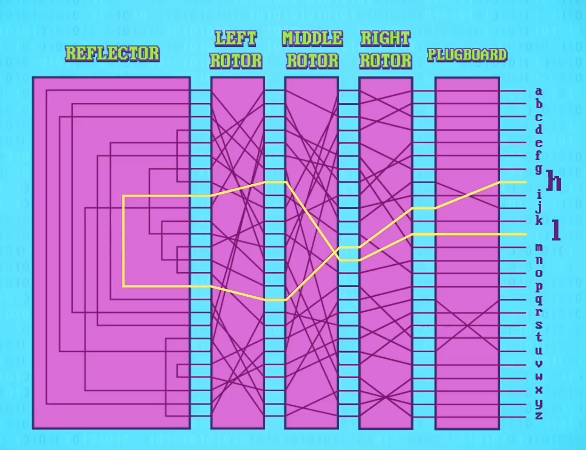
注意，电路是 双向 的，所以如果我们按下 L ， H 会亮起来，也就是 L 变 H ， H 变 L 。

换句话说，加密和解密的步骤是 一样 的，你只需要确保发送机和接收机的初始 配置 一样就行，如果你有仔细观察，会注意到字母加密后一定会变成另一个字母，之后这成为最大的弱点。

最后，为了让英格玛 不只 是简单的 替换加密 ，每输入一个字母，转子会转一格，有点像汽车里程表。

如果你输入 A-A-A ，可能会变成 B-D-K ，映射会随着每次按键而改变。

英格玛当然是一块难啃的骨头，但正如我们之前说的， 艾伦·图灵 和同事破解了英格玛加密，并把大部分破解流程做成了 **自动化 ** 。

DES ​

但随着计算机出现，加密从硬件转往 软件 ，早期加密算法中，应用最广泛的是 IBM 和 NSA 于 1977 年开发的 数据加密标准 （Data Encryption Standard），简称 DES 。

DES 最初用的是 56bit 长度的二进制密钥，意味着有 2 的 56 次方，或大约 72 千万亿个 不同 密钥。

在 1977 年时，也许 NSA 有这能力，但没有其他人有足够计算能力来暴力破解所有可能密钥。

AES ​

但到 1999 年，一台 25 万美元的计算机能在两天内，把 DES 的所有可能密钥都试一遍，让 DES 算法不再安全，因此 2001 年出了： 高级加密标准 （Advanced Encryption Standard），简称 AES 。

AES 用更长的密钥，128 位 / 192 位 / 256 位，让暴力破解更加困难，128 位的密钥，哪怕用现在地球上的所有计算机，也要上万亿年才能试遍所有组合。

AES 将数据切成一块一块，每块 16 个字节，然后用密钥进行 一系列 替换加密和移位加密，再加上一些其他操作，进一步加密信息，每一块数据，会重复这个过程 10 次或以上，你可能想知道：为什么只重复 10 次？为什么用 128 位密钥，而不是 10000 位？

这其实是基于性能的 权衡 ，如果要花几小时加密和发邮件，或几分钟载入网站，没人愿意用， AES 在性能和安全性间取得平衡。

如今 AES 被广泛使用，比如 iPhone 上加密文件，用 WPA2 协议 在 WiFi 中访问 HTTPS 网站。

密钥交换 ​

到目前为止我们讨论过的加密技术，依赖于发送者和接收者 都知道 密钥，发件人用密钥加密，收件人用相同的密钥解密，以前，密钥可以口头约定，或依靠物品。

比如德国人给英格玛配了密码本，上面有每天的配置，但互联网时代没法这样做。

我们需要某种方法在公开的互联网上传递密钥给对方，这看起来好像不安全，如果密钥被黑客拦截了，黑客不就能解密通信了吗？

解决方案是 密钥交换 （key exchange）。

密钥交换是一种 不发送 密钥，但依然让两台计算机在密钥上达成共识的算法。

我们可以用 单向函数 （one-way functions）来做，单项函数是一种数学操作，很容易算出结果，但想从结果 逆向 推算出输入非常困难。

为了让你明白单项函数，我们拿颜色作比喻，将颜色混合在一起很容易，但想知道混了什么颜色很难，要试很多种可能才知道。

用这个比喻，那么我们的密钥是一种 独特 的颜色。

对称加密 ​

首先，有一个公开的颜色，所有人都可以看到，然后，John 和我 各自 选一个秘密颜色，只有自己知道。

为了交换密钥，我把我的秘密颜色和公开颜色混在一起，然后发给 John ，可以写信发，用信鸽发，什么方式都行。

John 也这样做，把他的秘密颜色和公开颜色混在一起，然后发我。

我收到约翰的颜色之后，把我的秘密颜色加进去，现在 3 种颜色混合在一起，John 也一样做。

我们有了一样的颜色，我们可以把这个颜色当密钥，尽管我们从来没有给对方发过这颜色，外部窥探者可以知道部分信息，但无法知道最终颜色。

迪菲-赫尔曼密钥交换 ​

当然，计算机要传输数据时，混合颜料和发颜料不太合适，但幸运的是，数学单向函数是完美的，我们可以用 迪菲-赫尔曼密钥交换 （Diffie-Hellman Key Exchange）。

在 Diffie-Hellman 中，单向函数是 模幂运算 ，意思是先做幂运算，拿一个数字当底数，拿一个数字当指数，比如 A 的 B 次 ，然后除以第三个数字，最后拿到我们想要的余数。

举个例子，假设我们想算 3 的 5 次方，模 31 。

我们先算 3 的 5 次方，得到 243 ，然后除 31 ，取余数，得到 26 ，重点是如果只给 余数 和 基数 ，很难得知 指数 是多少。

如果我告诉你，3 的某次方模 31，余数是 7 ，你要试很多次，才能知道次方是多少。

如果把数字变长一些，比如几百位长，想找到秘密指数是多少，几乎是不可能的。

现在我们来讨论 Diffie-Hellman 是怎么，用模幂运算算出双方共享的密钥。

首先，我们有公开的值，基数和模数，就像公开的油漆颜色，所有人都看的到，甚至坏人!

为了安全向 John 发信息，我选一个秘密指数：X，然后算 B^X mod M 的结果。

然后把这个大数字发给 John ， John 也一样做，选一个秘密指数 Y ，然后把 B^Y mod M 的结果发我。

为了算出双方共用的密钥，我把 John 给我的数，用我的秘密指数 X ，进行模幂运算，数学上相等于 B 的 XY 次方模 M 。

John 也一样做，拿我给他的数进行模幂运算，最终得到 一样 的数，双方有一样的密钥，即使我们从来没给对方发过各自的秘密指数。

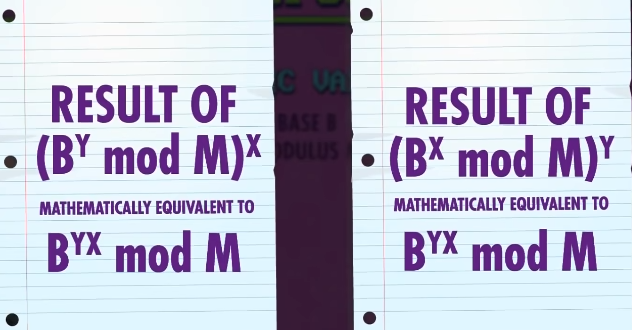
我们可以用这个大数字当密钥，用 AES 之类的加密技术来加密通信， Diffie-Hellman密钥交换 是建立共享密钥的一种方法。

双方用一样的密钥加密和解密消息，这叫 对称加密 （symmetric keys），因为密钥一样，凯撒加密，英格玛，AES 都是 对称加密 。

非对称加密 ​

还有 非对称加密 （asymmetric encryption），有两个 不同 的密钥，一个是公开的，另一个是私有的。

人们用公钥加密消息，只有有私钥的人能解密，换句话说，知道公钥只能加密但不能解密，它是 不对称 的！

想象一个可以锁上的盒子，为了收到安全的信息，我们可以给别人箱子和锁，别人把信息放箱子，然后锁起来，把盒子寄回给我，只有我的钥匙能打开，上锁后，如果发件人或其他人想打开盒子，除了暴力尝试没有其他办法。

和盒子例子一样，公钥加密后只能私钥来解密，反过来也是可以的，私钥加密后用公钥解密。

这种做法用于 签名 ，服务器可以用私钥加密，任何人都可以用服务器的公钥解密，就像一个不可伪造的签名，因为只有私钥的持有人能加密。

RSA ​

这能证明数据来自正确的服务器或个人，而不是某个假冒者，目前最流行的 非对称加密 技术是 RSA ，名字来自发明者：Rivest ，Shamir ，Adleman 。

现在你学会了现代密码学的所有 关键 部分： 对称加密，密钥交换，公钥密码学 。

当你访问一个安全的网站，比如银行官网，绿色锁图标代表用了公钥密码学。

验证服务器的密钥，然后建立临时密钥，然后用对称加密保证通信安全，不管你是网上购物，发邮件给朋友，还是看猫咪视频，密码学都在保护你的隐私和安全。