计算机科学入门
布尔代数
布尔代数名字来源于乔治·布尔,19世纪最重要的数学家之一,出版了《逻辑的数学分析》 ,这是他对符号逻辑的第一次贡献。1854年,他出版了《思维规律的研究》,这是他最著名的著作。在这本书中布尔介绍了现在以他的名字命名的布尔代数。

在高中数学的第一节课我们就学习了布尔代数中的集合运算: 交集、并集、补集 。
而现在将要介绍布尔代数中的剩下一个部分逻辑运算: 与(AND)、或(OR)、非(NOT) 。
在数学中代数最常见的是 x ,当然还有非常多的代数,而在逻辑运算中只有两个: true 、 false 。
| 逻辑运算 | 布尔运算 | 命题逻辑 |
|---|---|---|
| NOT(非;取反) | ~ | ¬ |
| AND(与) | & | ∧ |
| OR(或) | | | ∨ |
基础运算
NOT
TIP
这个比较特殊,只需要一个输入即可。
把布尔值反转,把 true 进行 NOT 就会变成 false,反之亦然
| 输入 | 输出 |
|---|---|
| True | False |
| False | True |
像这种 表征逻辑事件输入和输出之间全部可能状态的表格 ,我们将它称为 真值表 。
AND
只有两个 均为 True 才为 True 。
| 输入A | 输入B | 输出Y |
|---|---|---|
| False | True | False |
| False | True | False |
| True | False | False |
| True | True | True |
OR
两个 其中之一 为 Ture 则为 True 。
| 输入A | 输入B | 输出Y |
|---|---|---|
| False | False | False |
| False | True | True |
| True | False | True |
| True | True | True |
逻辑门
我们先来看一道 初中 电路基础题。

很容易看出这道题选 A ,因为电流从正极流出之后会选择电阻为零的那一条路, L2 被短路了。
电路其实就跟公路一样。一个是人走的,一个是电子走的。当路径最短且最通畅时,你开车时自然就选择了这条路。
NOT 非门
当输入为真时,电流将不会流过 OUTPUT ,因此 OUTPUT 为假。
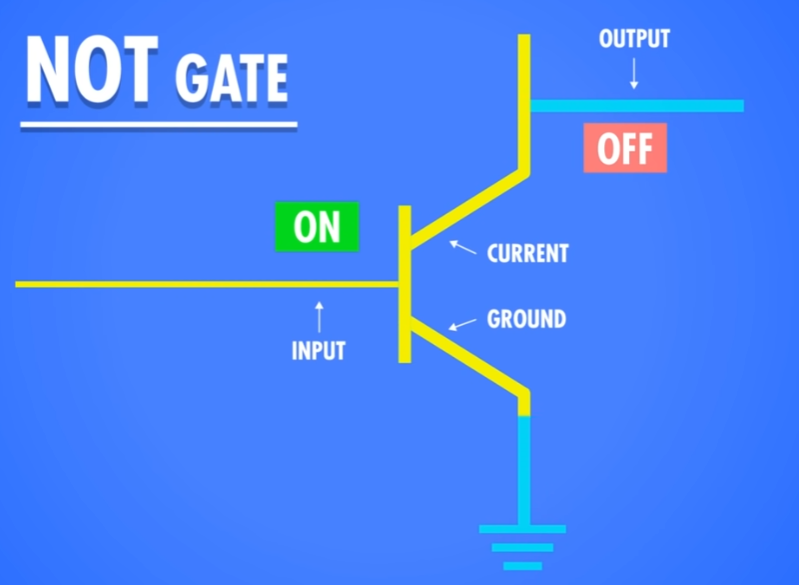
当输入为假时,电流无法流过,因此 OUTPUT 为真。
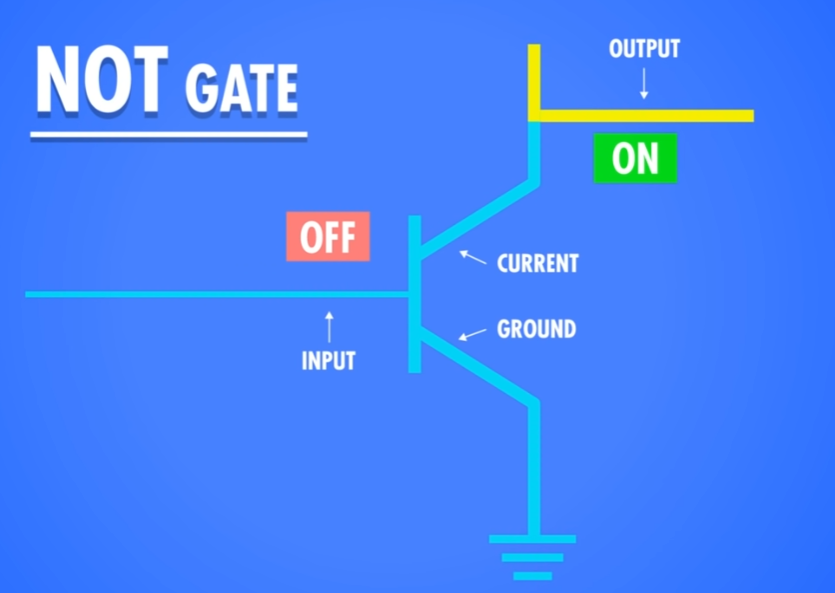
CMOS 电路:
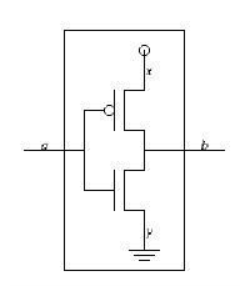
太复杂了,它可以这样表示:
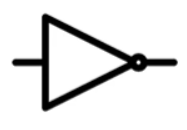
真值表
| 输入 | 输出 |
|---|---|
| True | False |
| False | True |
AND 与门
仅打开 A ,电流无法流过。
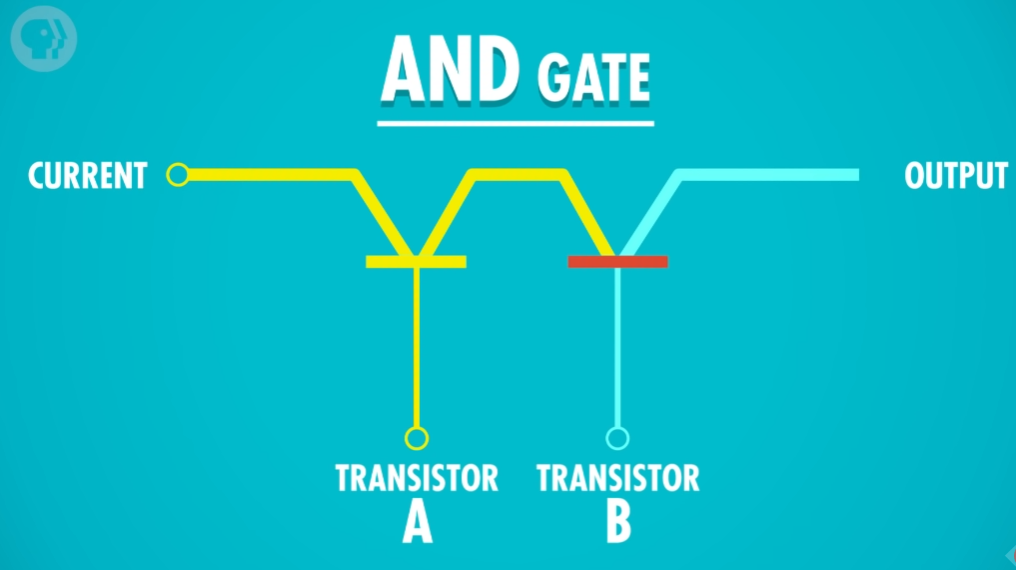
仅打开 B 也是同理。
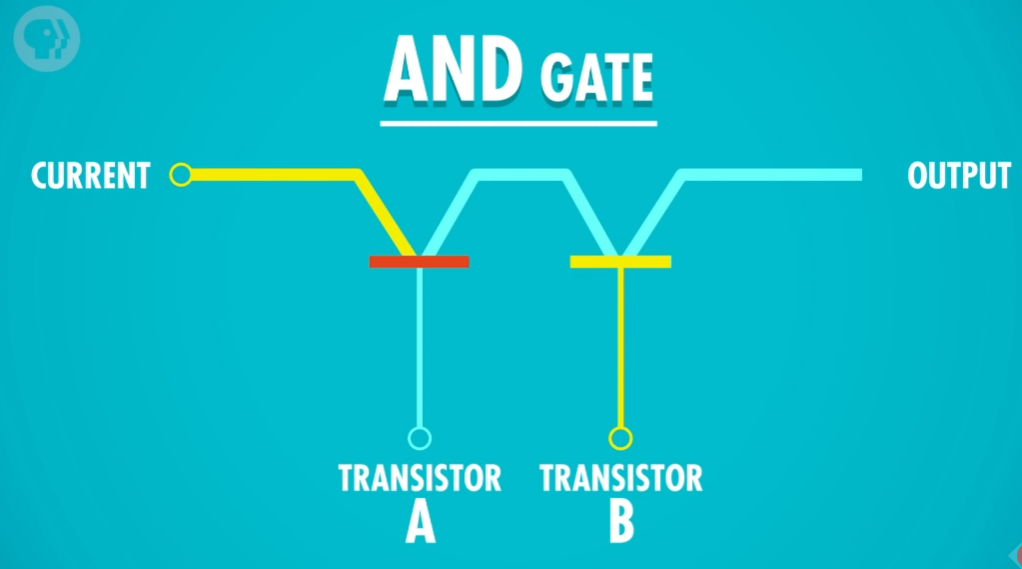
只有 同时 打开 A 和 B ,电流才能通过。
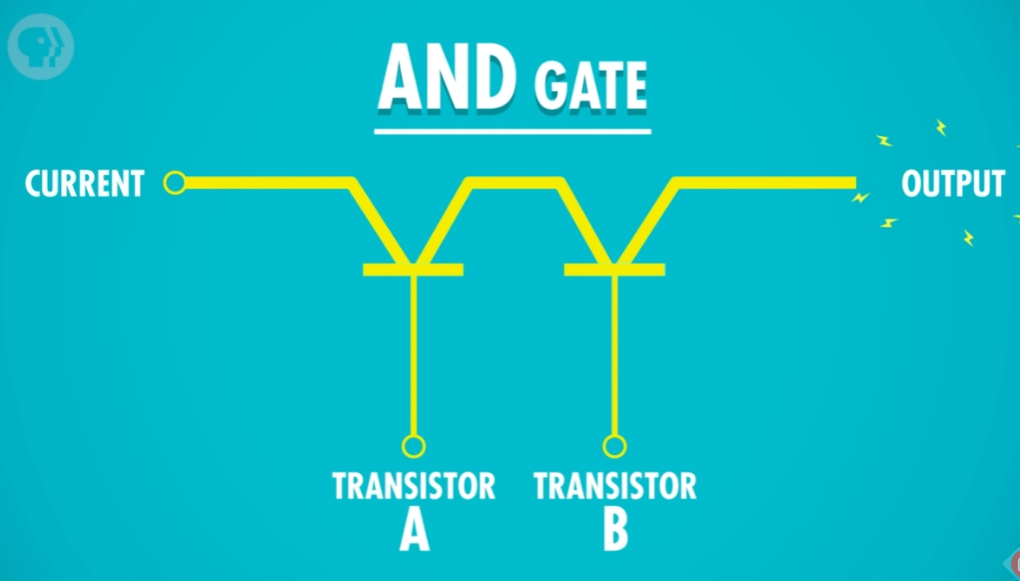
CMOS 电路:
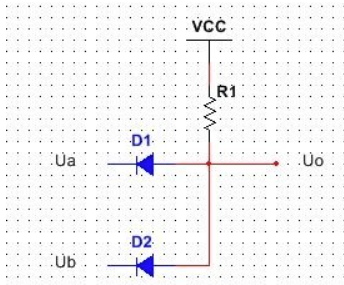
太复杂了,它可以这样表示:

真值表
| 输入A | 输入B | 输出Y |
|---|---|---|
| False | True | False |
| False | True | False |
| True | False | False |
| True | True | True |
OR 或门
可以把它看成是 非门 和 与门 的并联。
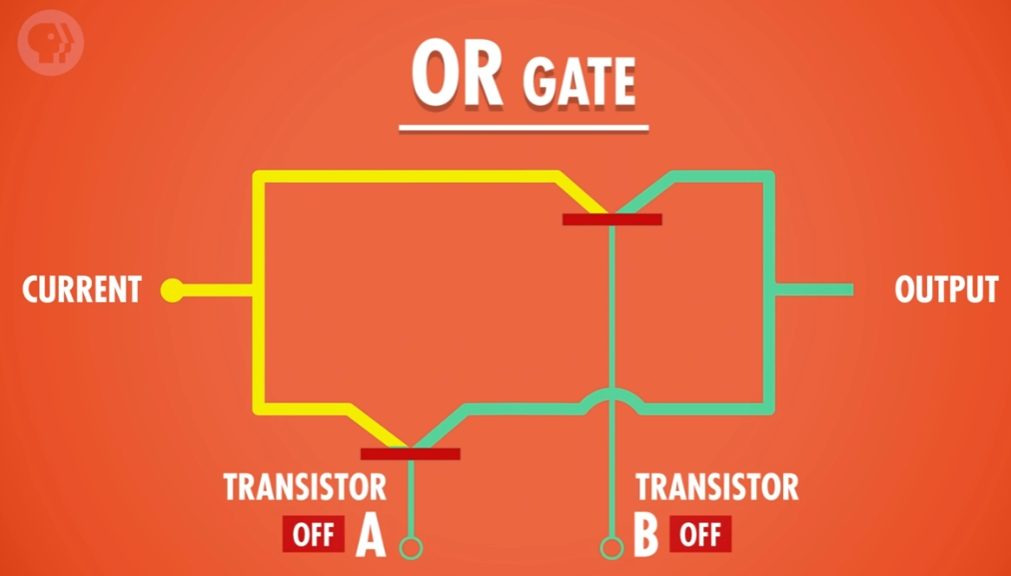
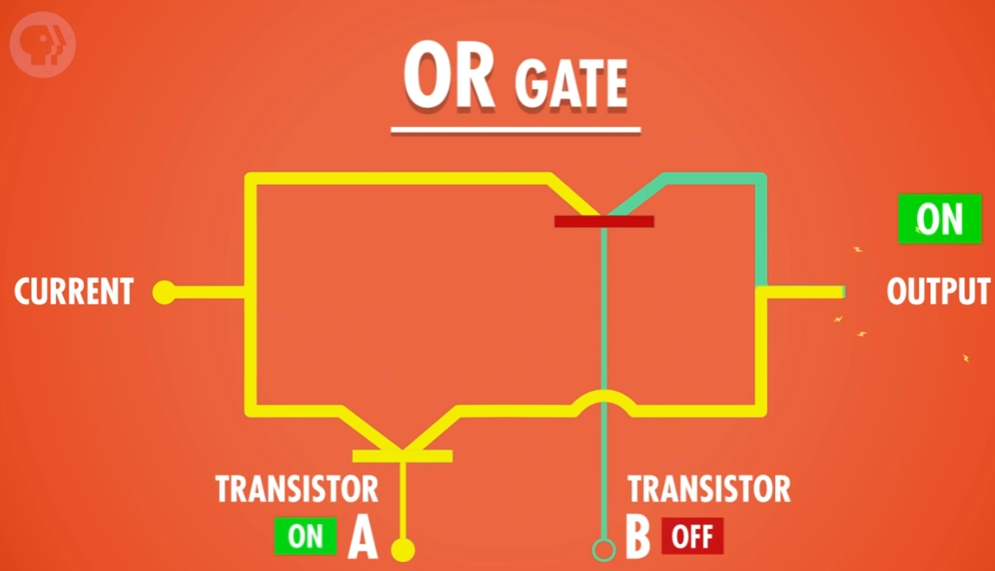
如果仅打开 A ,电流可以通过。
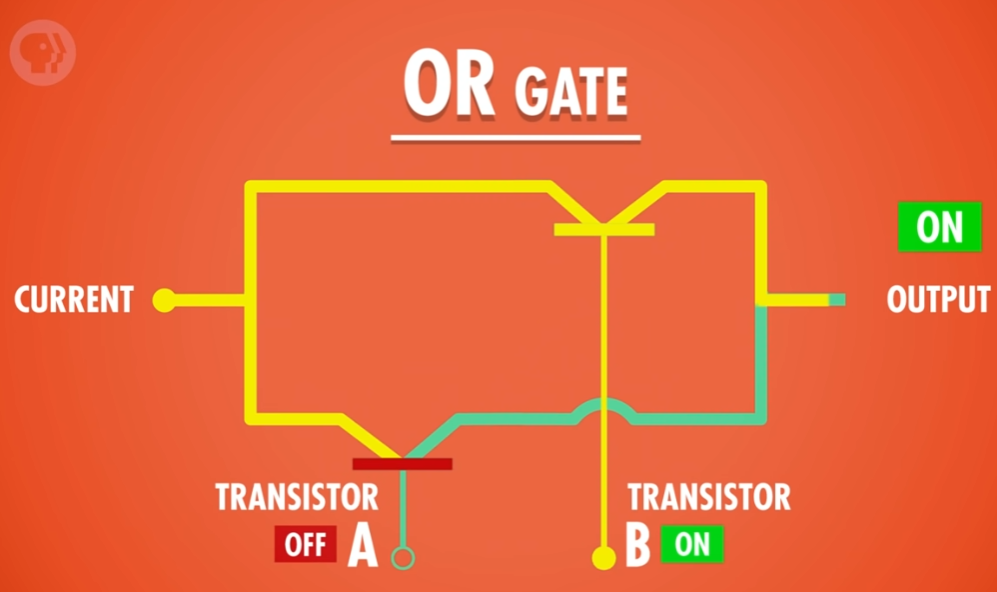
如果仅打开 B ,电流也可以通过。
CMOS 电路:
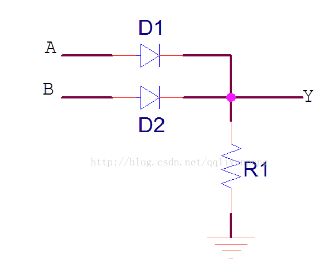
太复杂了,它可以这样表示:
真值表
| 输入A | 输入B | 输出Y |
|---|---|---|
| False | False | False |
| False | True | True |
| True | False | True |
| True | True | True |
XOR 异或门
它和或门的唯一区别就是,当输入均为 True 的时候,输出 False 。
真值表
| 输入A | 输入B | 输出Y |
|---|---|---|
| False | False | False |
| False | True | True |
| True | False | True |
| True | True | False |
想要实现这种效果我们可以从 或门 开始:
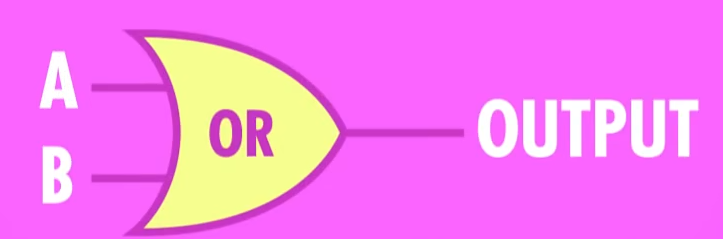
我们可以加一个 与门 ,但是这样依然是 True :
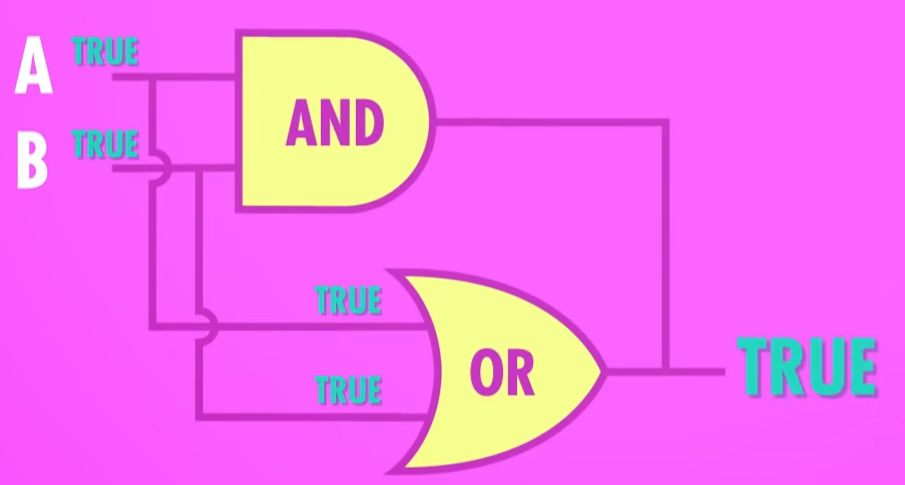
在与门后面加一个 非门 ,这样就有 False 了:
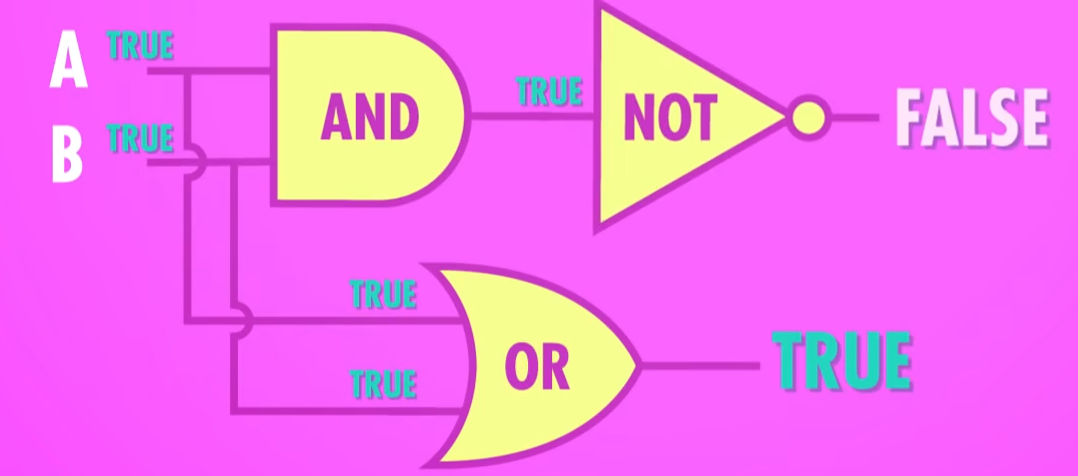
我们需要的是 False ,所以需要结合一个 与门 :
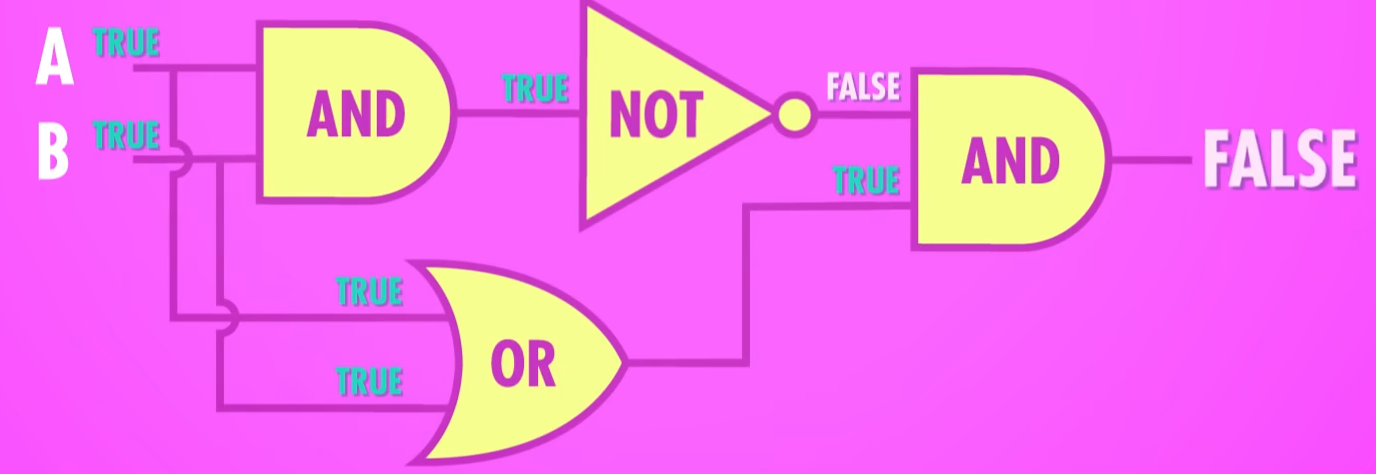
验证真值表中的其他几行,也一样符合。
它可以这样表示:
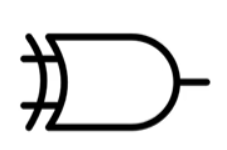
XNOR 同或门
在 异或门 后面再加一个 非门 就成了 同或门 。

真值表
| 输入A | 输入B | 输出Y |
|---|---|---|
| False | True | True |
| False | True | False |
| True | False | False |
| True | True | True |
NOR 或非门
在 或门 后面再加一个 非门 就成了 或非门 。

真值表
| 输入A | 输入B | 输出Y |
|---|---|---|
| False | False | True |
| False | True | False |
| True | False | False |
| True | True | False |
NAND 与非门
在 与门 后面再加一个 非门 就成了 与非门 。

真值表
| 输入A | 输入B | 输出Y |
|---|---|---|
| False | False | True |
| False | True | True |
| True | False | True |
| True | True | False |